Table of Contents
Trigonometry Math Problem – 2
Given the Tri-Tangent Circle with Radius 30mm and the Angle Theta with value of 20deg. find the length X.
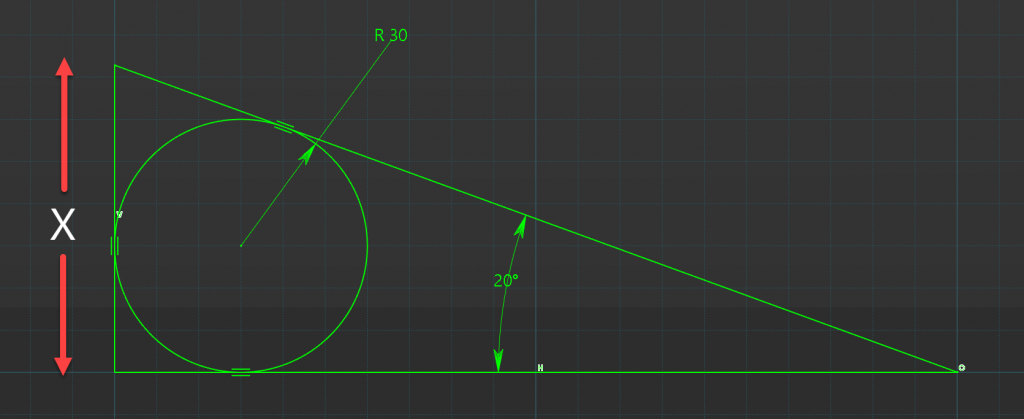
Tricky Triangle Trigonometry Constants
Things we know about Tri-Tangent circles within a Triangle, all angles can be bisected by drawing lines from the triangle corners to the circle center.
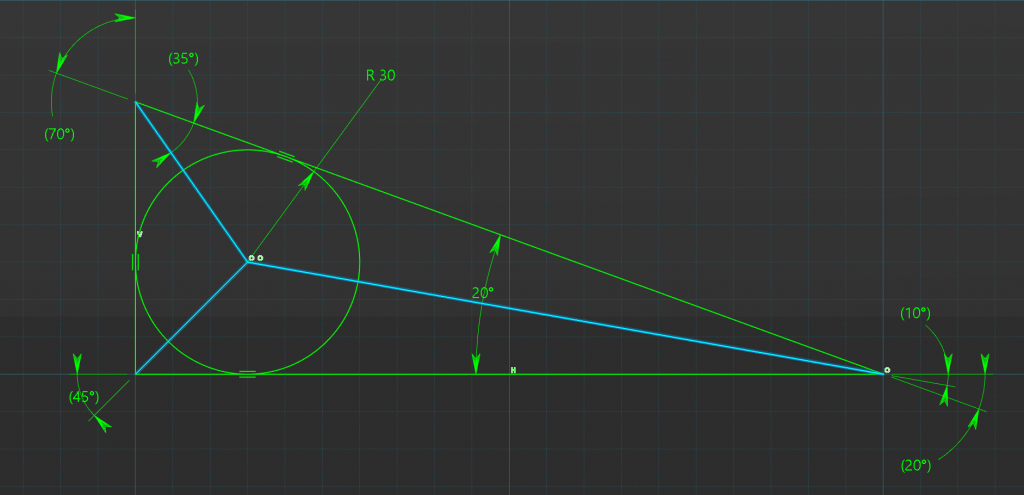
Lines perpendicular to each side through the circle center produce, addition right-angled triangles.

Finally all internal Right-Angled Triangles have one side which is equivalent to the radius of the circle.
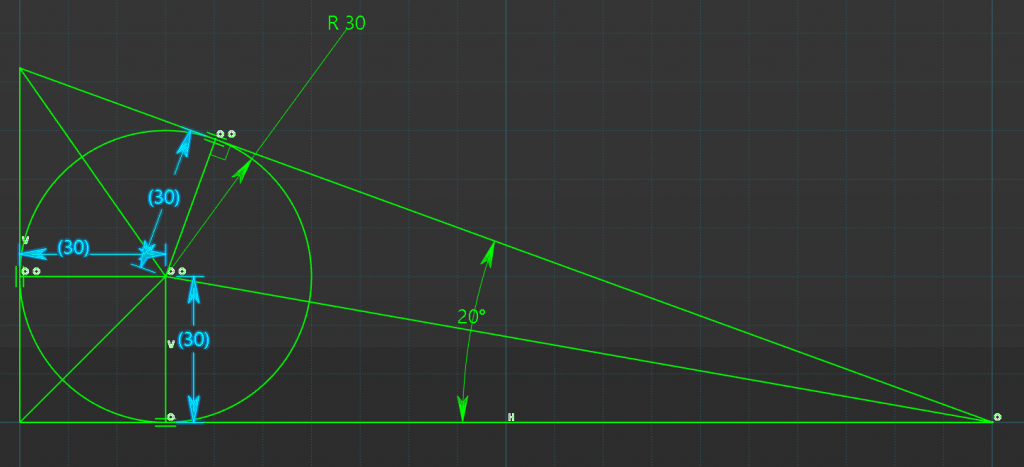
Solving the Sub Triangles
Given These three facts we can solve each internal triangle to finally solve the main external triangles size.
Triangle One
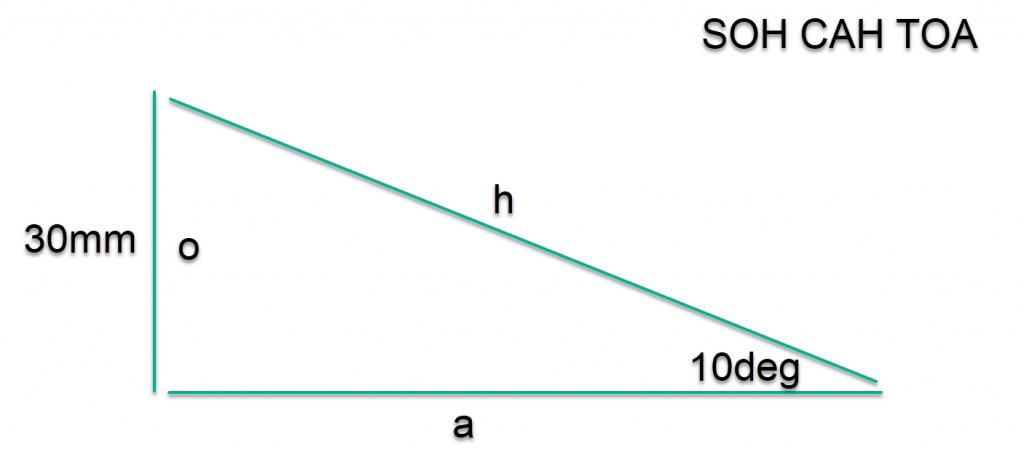
Lets start of with this triangle
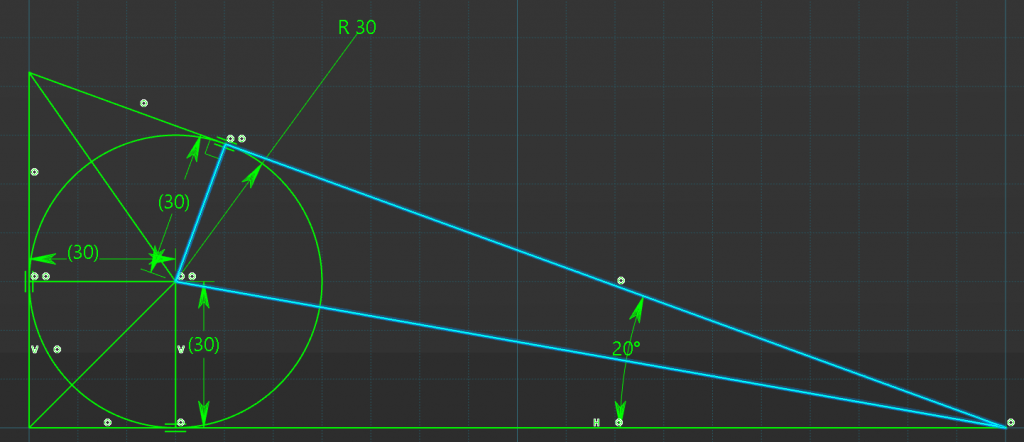
Lets redraw it.
Since we know the length of the side opposite the angle and we need ‘a’, we can derive from SOH, CAH,TOA that this is a Tan problem.
tan(theta) = O / A \\ tan(10deg) = 30mm / A \\ A = 30mm / tan(10deg) \\ A = 30mm / 0.17632 \\ A = 170.1384mm
And were correct compared to CAD
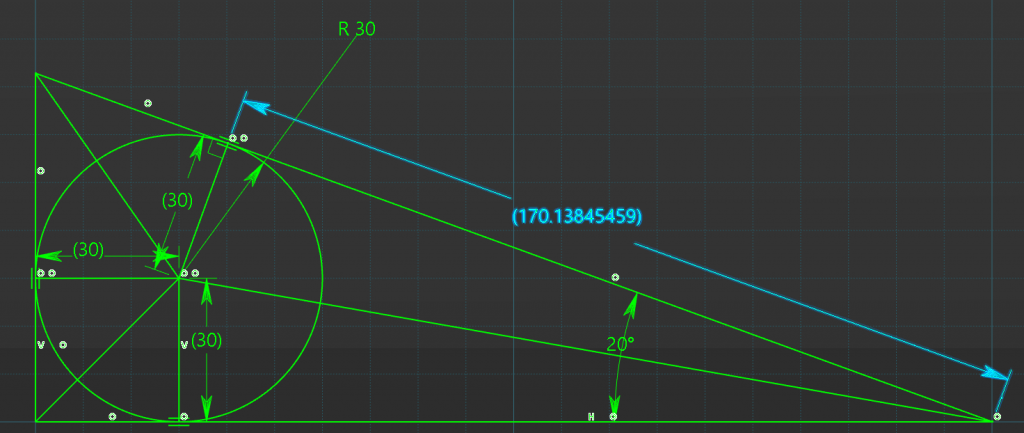
Triangle Two
Lets complete the first side by calculating the next triangle.
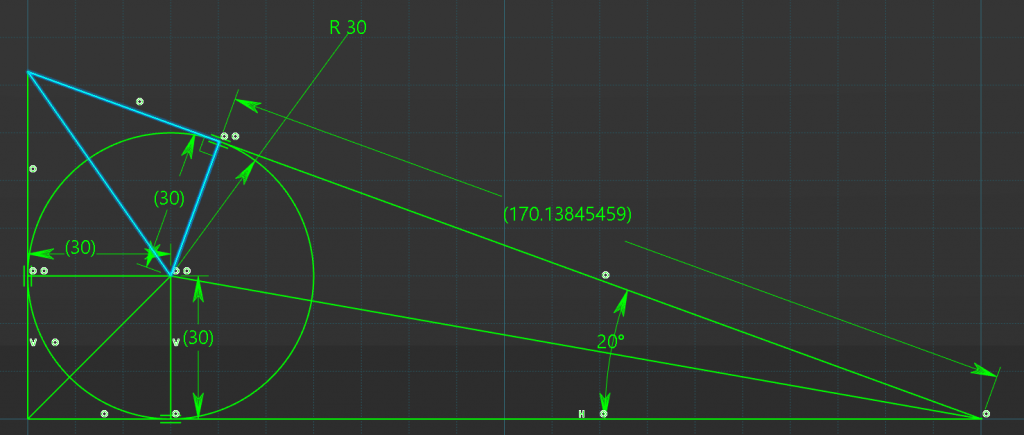
To do this we know that a triangle has a total internal angle of 180deg. Therefor the top left corner must be (180deg – (20deg + 90deg)) = 70deg. For the external triangle but for the smaller internal triangle we must divide by 2 = 35degrees, now we have enough information to proceed.
tan(theta) = O / A \\ tan(35deg) = 30mm / A \\ A = 30mm / tan(35deg) \\ A = 30mm / 0.7002 \\ A = 42.8444mm
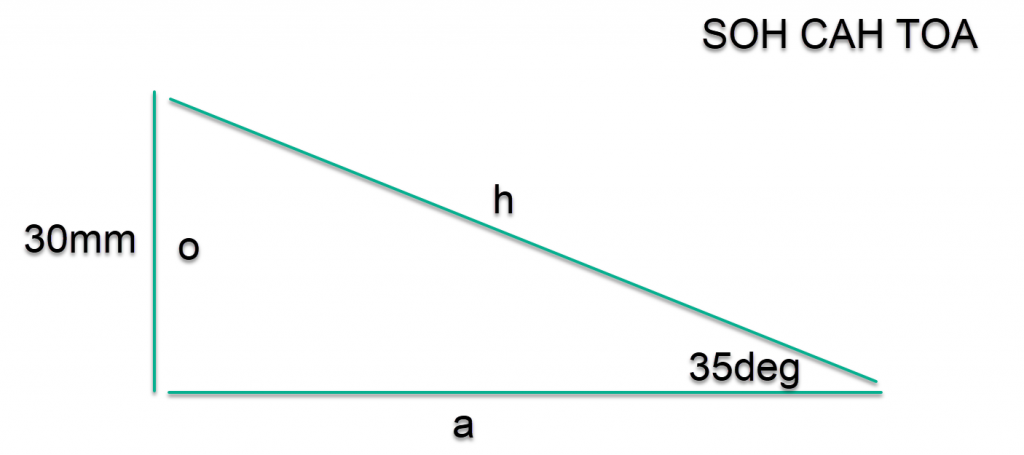
And again were correct compared to CAD.
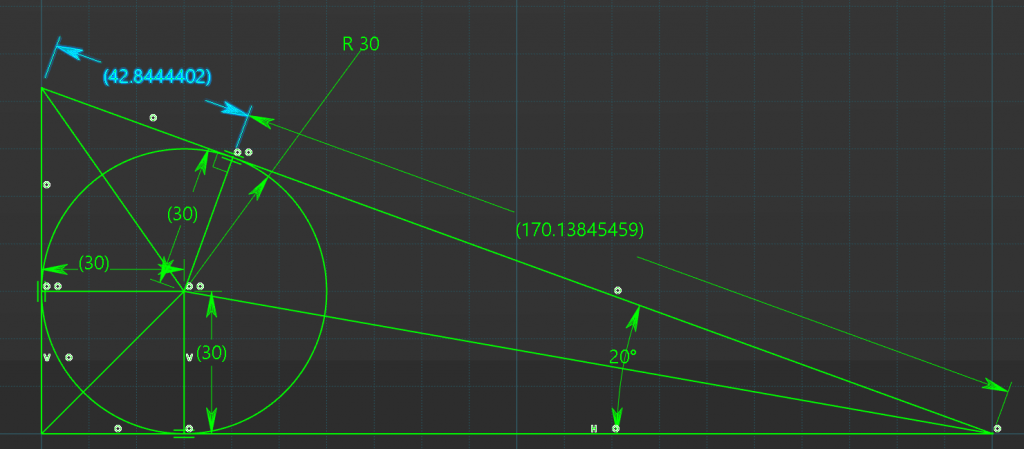
Hypotenuses Length
We can now add the two lengths together to get the complete length of the side
42.8444mm + 170.1384mm = 212.9828mm
or the equation will be;
Hyp = (30mm / tan(10deg)) + (30mm / tan(35deg)) \\ Hyp = (30mm / 0.17632) + (30mm / 0.7002) \\ Hyp = 170.1384 + 42.8444 \\ Hyp = 212.9828mm
Triangle Three
Triangle three is really simple its a symmetric triangle to the first triangle, so its hypotenuses length is the same as triangle 1, 170.1384mm
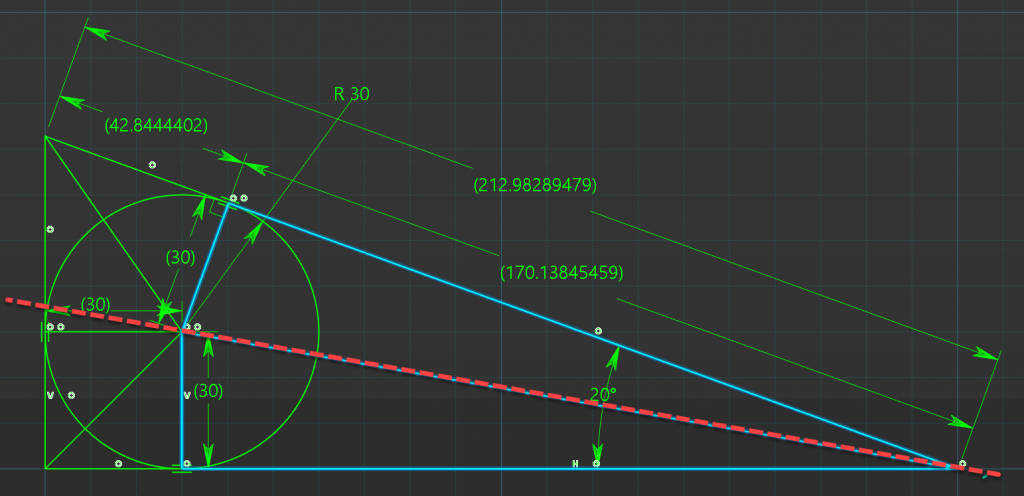
Triangle Four
And as for this one again were dealing with Tan, and its the 90deg external triangles corner which makes the internal triangles corner 45deg. Since it tan the tan of 45 is 1. There for the length is 30mm the same as the radius.
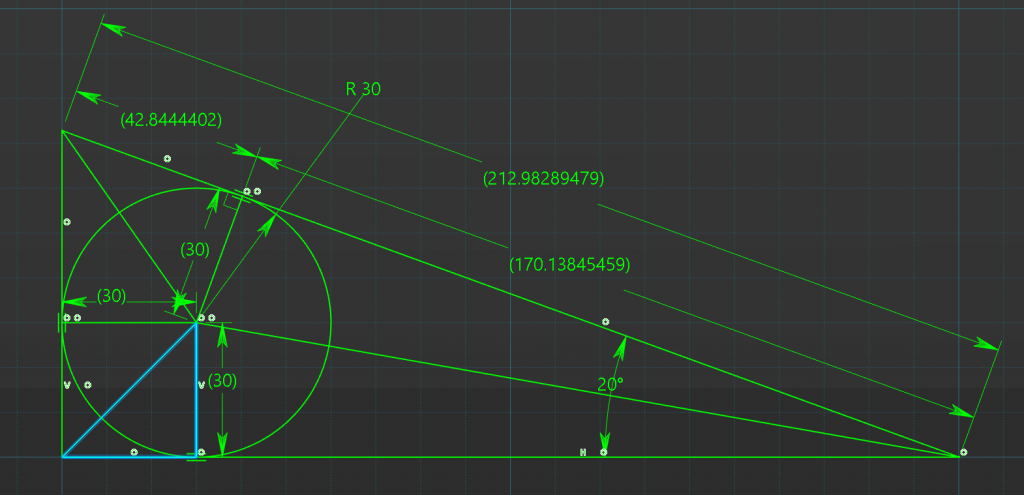
Base Length
As shown below we can now add the two lengths together to get the complete length of the side
30mm + 170.1384mm = 200.1384mm
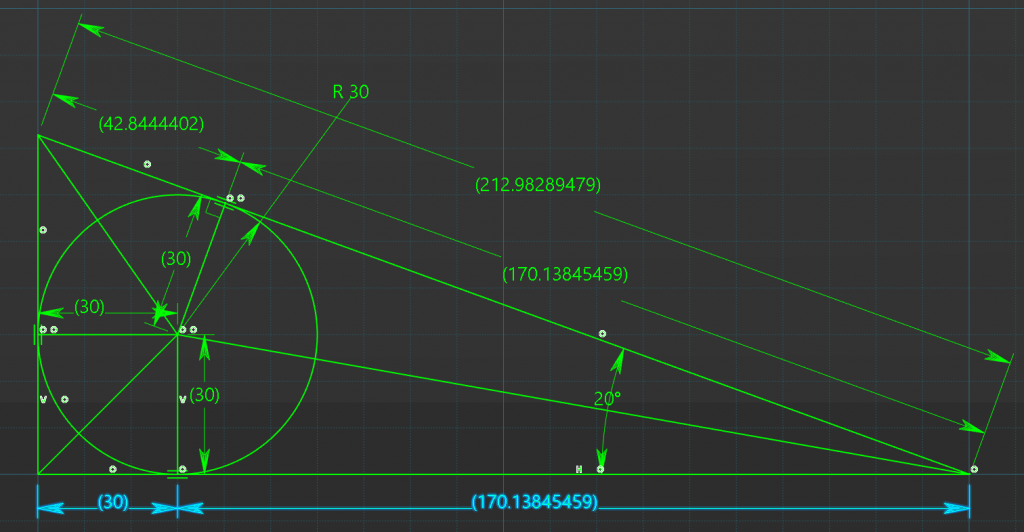
or the equation will be;
Base = ( 30mm / tan(10deg) ) + 30mm \\ Base = ( 30mm / 0.17632 ) +30mm \\ Base= 170.1384mm + 30mm \\ Base = 200.1384mm
Final Side
We know from Pythagorean theorem that the Hyp = Sqrt( Opp^2 + Base^2 ) we can use this equation by re-arranging it since we have the Hypotenuses and the Base lengths.
Opposite = \sqrt{ Hyp^2 - Base^2 } \\
Opposite = \sqrt{ 212.9828^2 - 200.1384^2 } \\
Opposite = \sqrt{ 45,361.6730 - 40,055.3791 } \\
Opposite = \sqrt{ 5,306.2939 } \\
Opposite = 72.8443mm
Here is the final CAD Validation,
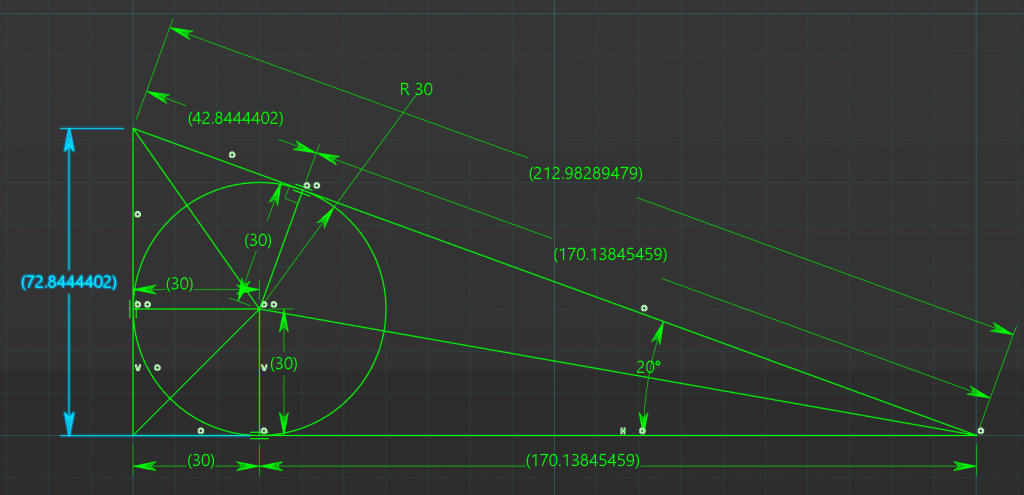
We can also rearrange all the equation into one equation.
Opposite = \sqrt{ ((30mm / tan(10deg)) + (30mm / tan(35deg)))^2 - (( 30mm / tan(10deg) ) + 30mm)^2 } \\
Opposite = \sqrt{ 212.9828^2 - 200.1384^2 } \\
Opposite = \sqrt{ 45,361.6730 - 40,055.3791 } \\
Opposite = \sqrt{ 5,306.2939 } \\
Opposite = 72.8443mm