Table of Contents
Resolving Point Loads on a Beam
In this example we will see how to resolve the resultant loads at A and B due to the point load.
1 Tonnes in Kips = 2.2046
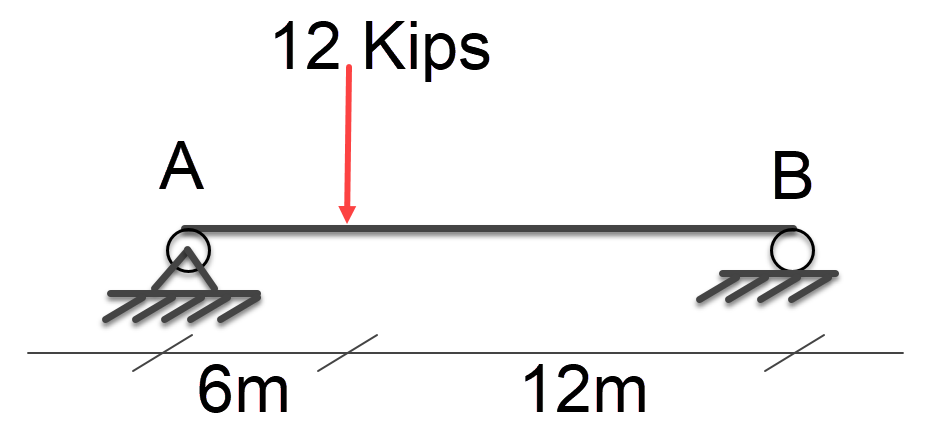
Free Body Diagram
First we will create a free body diagram, to represent our problem.
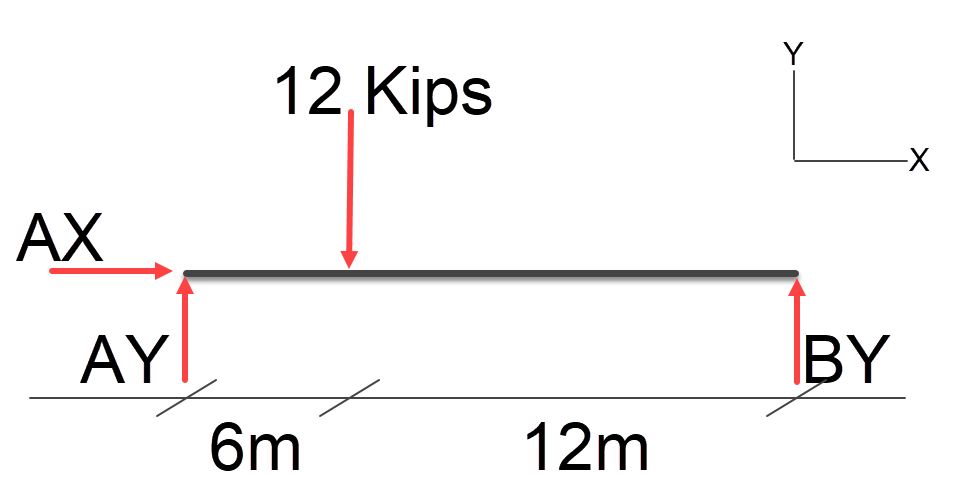
Calculations
It’s important to note that the AX load is 0kips in this case since no loads have any horizontal component.
We will use ratios to calculate the resulting loads AY and BY.
If the point load was centered along the span we know the loads at AY and BY are symmetrical and exactly half the value of the point load. We can use this logic of ratios to calculate the loads when the point load is not centered.
Lets do a calculation assuming the load is centered;
1 / ( 6 + 12 ) = 0.055555 \\ 0.055555 * ((6 + 12) / 2) = 0.5 \\ 12kips * 0.5 = 6kips \\
So we have a 6Kip load at AY and BY.
Back to our example let’s do AY first using the same equation;
1 / ( 6 + 12 ) = 0.055555 \\ 0.055555 * 6 = 0.333333 \\ 12kips * 0.333333 = 3.999996kips \\ \approxeq 4kips
and now BY;
1 / ( 6 + 12 ) = 0.055555 \\ 0.055555 * 12 = 0.666666 \\ 12kips * 0.666666 = 7.99992kips \\ \approxeq 8kips
We can verify the result by adding AY + BY which must equal the point load 12 Kips and indeed 4kips + 8kips = 12kips, success.
If we had multiple loads we would resolve for each one and total the loads up at the end for AY and BY, let’s try one.
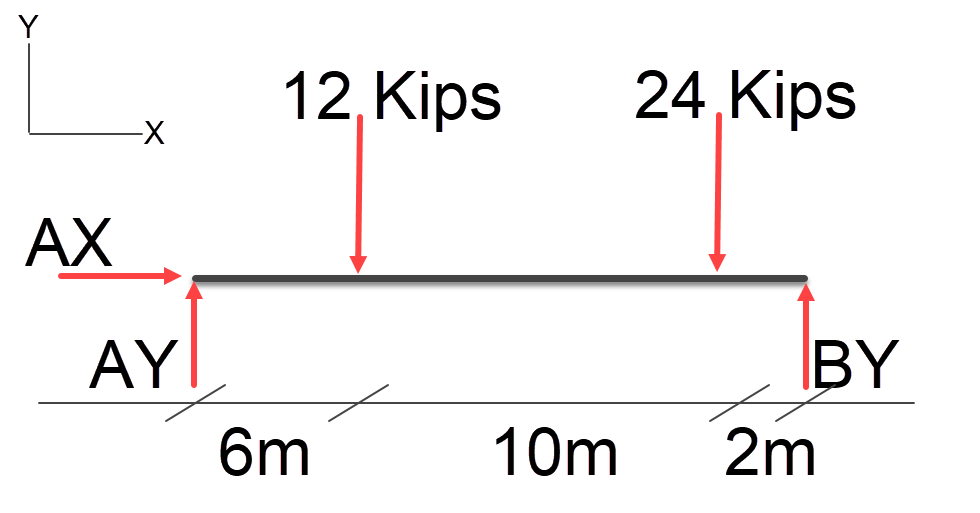
Let’s Calculate AY first;
1 / ( 6 + 10 + 2) = 0.055555 \\ 0.055555 * 6 = 0.333333 \\ 12kips * 0.333333 = 3.999996kips \\ and \\ 0.055555 * (6 + 10) = 0.888888 \\ 24kips * 0.888888 = 21.33333kips \\ so \\ 3.999996 + 21.33333 = 25.333329kips \\ \approxeq 25.3kips
and now BY;
1 / ( 6 + 10 + 2) = 0.055555 \\ 0.055555 * 12 = 0.666666 \\ 12kips * 0.666666 = 7.99992kips \\ and \\ 0.055555 * 2 = 0.11111 \\ 24kips * 0.11111 = 2.66664kips \\ so \\ 7.99992 + 2.66664 = 10.66656kips \\ \approxeq 10.7kips
and again finally to test we can verify the result by adding AY + BY which must equal the total point load 36Kips and indeed 25.3kips + 10.7kips = 36kips, success.
Making it Easier
Since we know that the sum of AY and BY must equal the sum of the point loads we can use this to our advantage.
If we calculate AY all we have to do to calculate BY is subtract AY from the sum of the point loads.
BY = \sum PointLoads - AY \\ BY = 36kips - 25.3kips \\ BY = 10.7kips
