Circle Diameter Math Problem
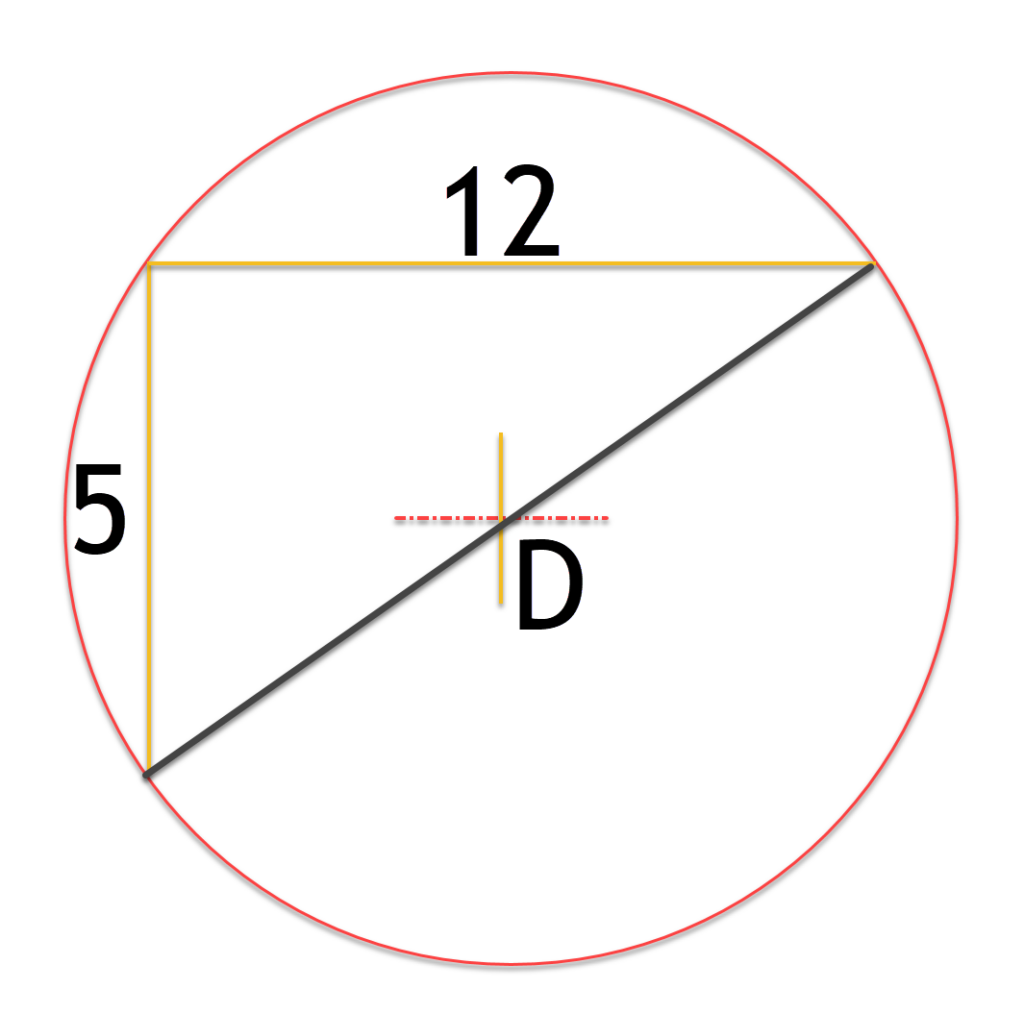
The diagram below shows a circle, with one chord and two lines with given lengths, we have to determine the circles radius.
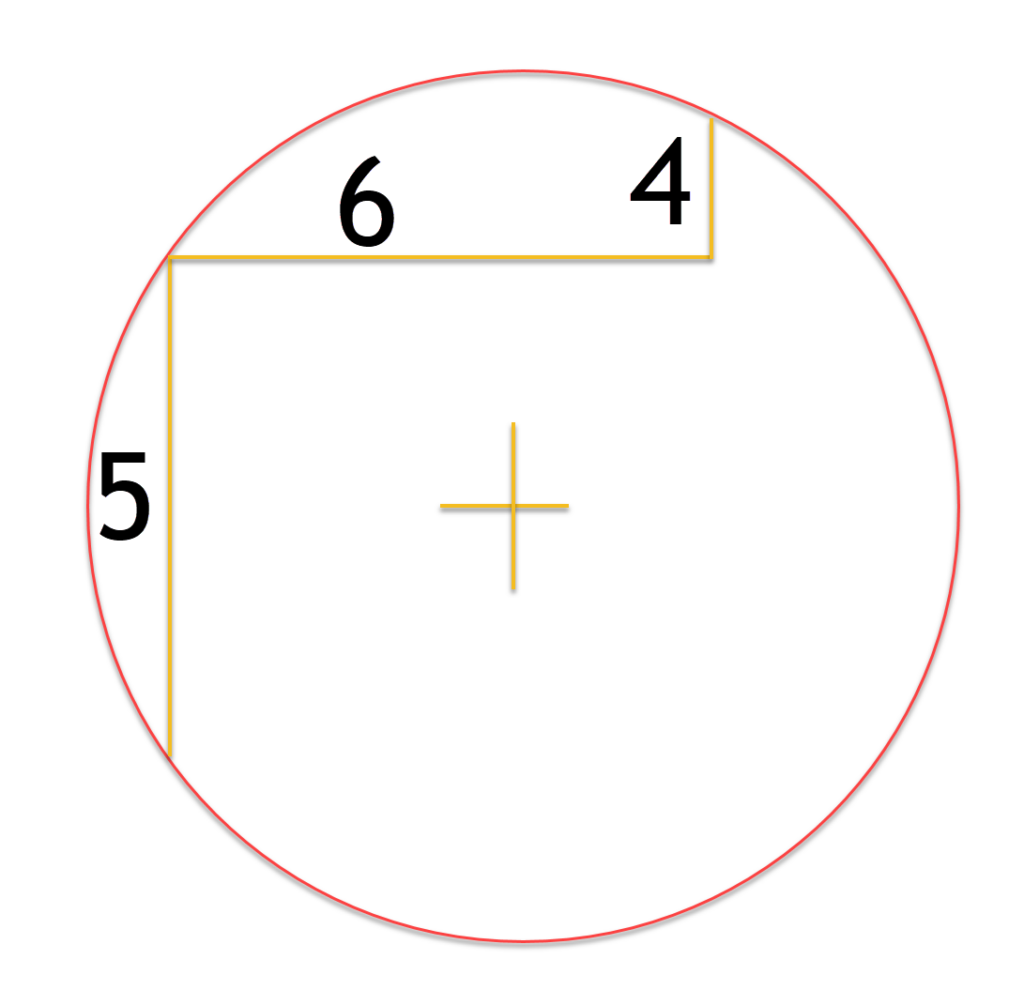
Since we know a line drawn perpendicular to a chord through the chords CenterPoint will always bi-sect the center of a circle we can establish a symmetrical bi-sector of the circle.
From this we can create symmetrical lines for the line of 6 units length and 4 units length, which allows us to determine a new chord of 4 + 5 + 4 or 13 units.
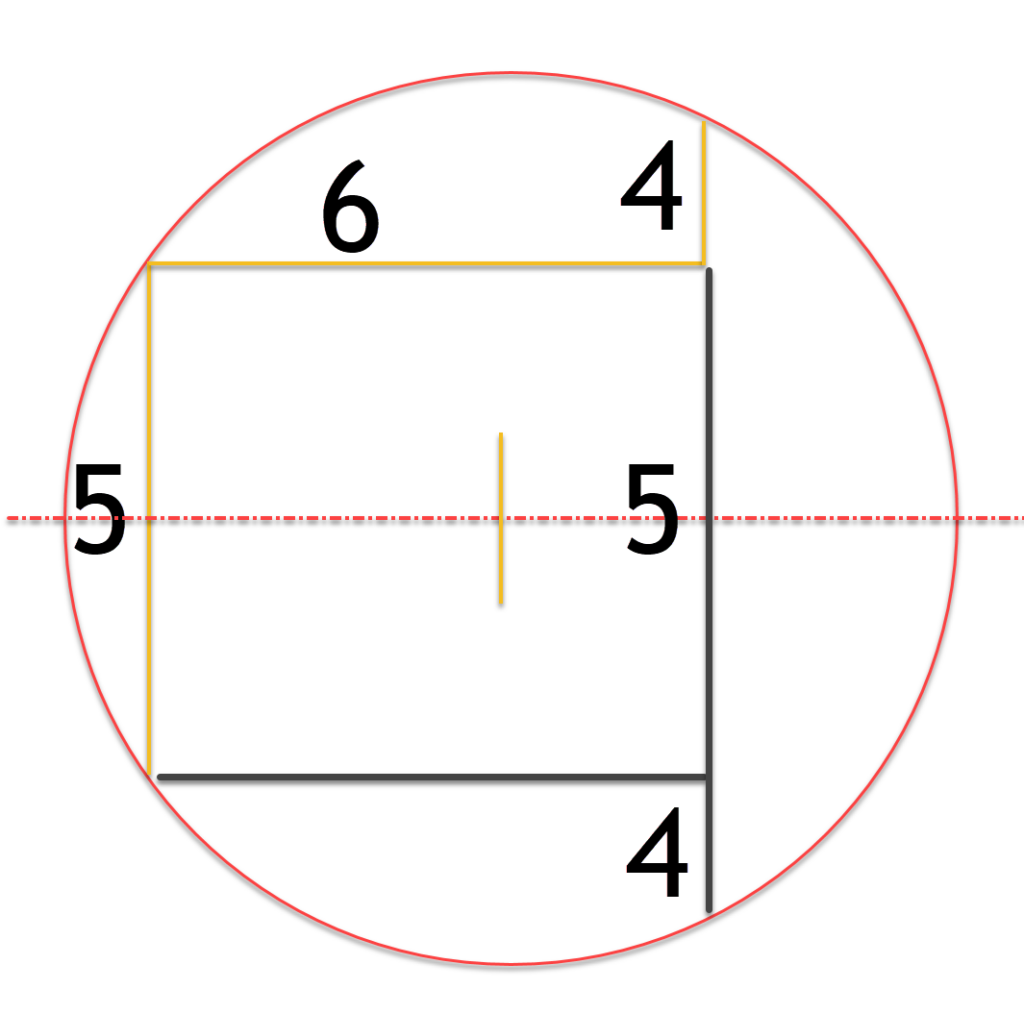
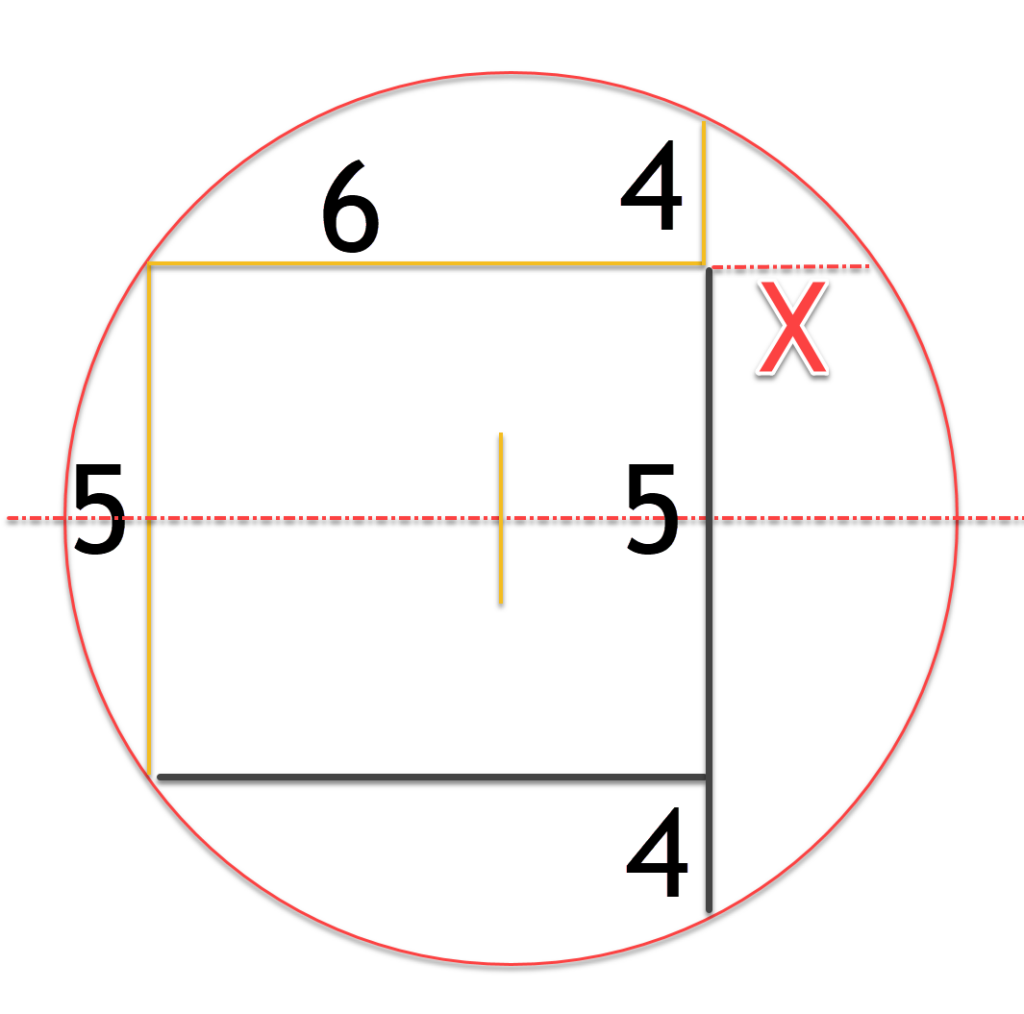
Now we can use the Chord Bi-Sector Theorem, which states that 6*X is the same as 4*(5+4).
So X = 4*(9)/6 = 6 units
Any Line that connect two perpendicular chords must pass through the center and is equivalent to the circles diameter. So we can easily use Pythagorean Theorem to calculate D = sqrt((12*12) + ( 5*5 )) = sqrt( 144 + 25 ) = sqrt (169) = 13 units.
Therefor R = 13/2 = 6.5units.