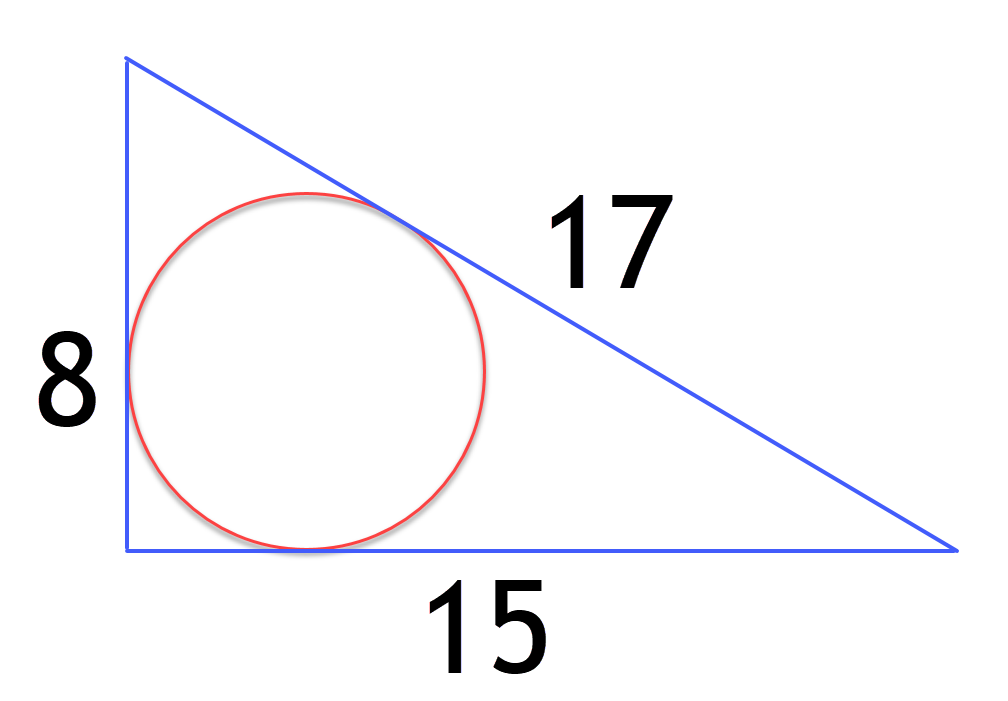
Area of An Inscribed Circle
I like these little geometry problems, they are a great way to learn geometrical math rules. So we need to calculate the area of the circle. We know that the area of a circle is PI*R^2 we know the value of CONST PI so all we need is the radius of the circle.
There is a simple derived formula to do this which is (A+B-C)/2 where C is the Hypotenuse and A and B are the length of the other two sides, but where does this equation come from.
The easy way to do this is to scribe two arcs.
From the two scribed arcs we can see that 17 = (8-R) + (15-R) which we can re-arrange as 17 = 8+15 – 2R, then 2R = 8+15-17 then if we divide both side by 2 we end up with R= (8+15-17)/2 therefore R = 3 and PI*3^2 = PI*9 = 9.425units^2
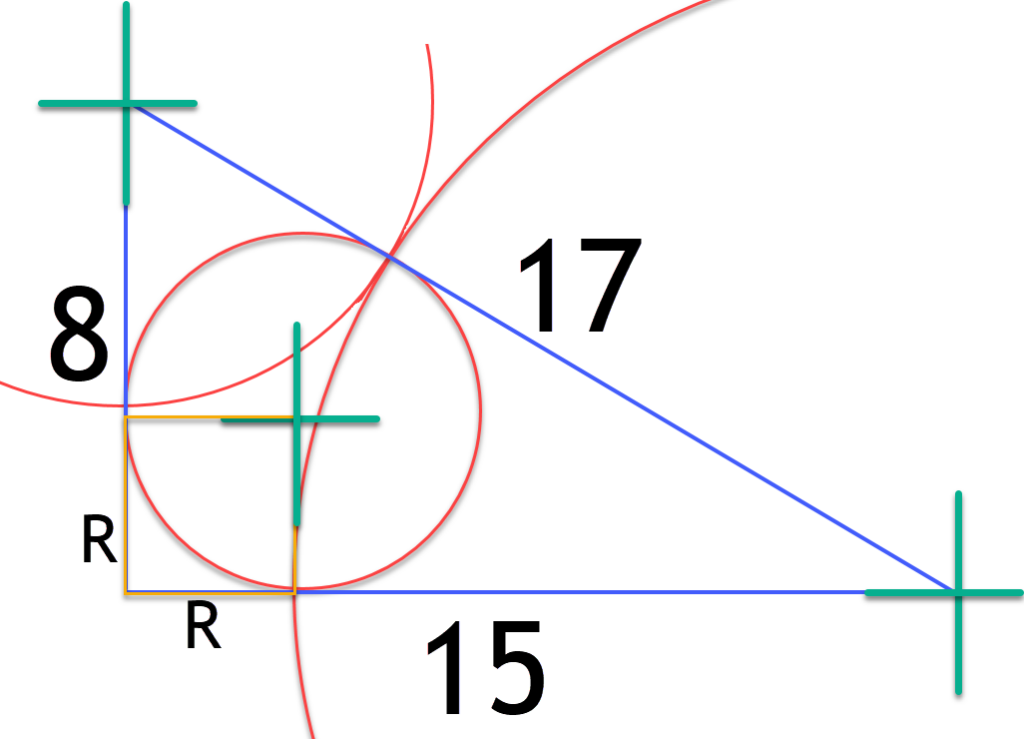
R= (8+15-17)/2 which is the same as writing R=(A+B-C)/2
